MATHEMATICAL MODEL OF DEEP CULTIVATION OF PLEUROTUS CITRINOPILEATUS BIOMASS
MATHEMATICAL MODEL OF DEEP CULTIVATION OF PLEUROTUS CITRINOPILEATUS BIOMASS
Abstract
This work is dedicated to the mathematical description of the conducted deep cultivation of such research object as PC-1.2 of xylotrophic basidiomycete Pleurotus citrinopileatus (P. citrinopileatus) – lemon oyster mushroom, pure culture of which was isolated from commercial fruiting bodies.
The experiment itself, deep cultivation, was carried out in a fixed laboratory bioreactor "CeCa-Cx650, UK" at 26 оC, pH 5.0 and continuous stirring by bubbling with sterile air.
The growth curve of Pleurotus citrinopileatus deep culture at inoculum concentration of 1 g/l was constructed on the basis of experimental data. It is shown that the growth curve is accurately described by the Mono equation. A mathematical model of deep culture growth was developed. Its homogeneity and adequacy have been checked. Application of the developed mathematical model allows to characterize the behaviour of the culture in deep conditions, to establish the optimal initial concentration of mycelium in the bioreactor, to predict the time and rate of accumulation of the maximum amount of biomass at different seeding concentrations.
1. Введение
В современном обществе белок является наиболее дефицитным компонентом пищи. Ценность пищевого белка определяется схожестью его аминокислотного состава с аминокислотным составом белков потребляющего его организма, что позволяет последнему активно усваивать и использовать подобные продукты в разнообразных метаболических процессах. В последние десятилетия значительное внимание исследователей в качестве продуцентов белка привлекают базидиальные грибы как источник белка, богатого незаменимыми аминокислотами.
Одним из перспективных продуцентов для получения грибного белка, является представитель рода Pleurotus – вешенка лимонная. Этот гриб, как в природных условиях, так и в культуре, непатогенен, обладает высокой пищевой ценностью и способен эффективно утилизировать разнообразные растительные субстраты.
Известно, что в плодовых телах вешенки лимонной (P. сitrinopileatus) наряду с белком, содержатся и биологически активные вещества, способные не только предупреждать, но и лечить широкий спектр заболеваний. Так, исследования последних лет , , свидетельствуют, что этот гриб обладает способностью снижать уровень глюкозы в крови человека, оказывает противоопухолевое действие, повышает иммунную устойчивость организма.
Сегодня показано, что культивируемый в глубинных условиях мицелий Pleurotus не уступает, а в ряде случаев по содержанию белка превосходит их плодовые тела , , . При этом глубинный мицелий имеет ряд преимуществ перед плодовым телом, из которых наиболее важные – чистота и стабильный химический состав. Таким образом, глубинное культивирование биомассы мицелия P. сitrinopileatus является одним из перспективных направлений получения пищевого и кормового белка , , .
Процесс получения мицелия по сравнению с выращиванием плодовых тел более высокопроизводителен при сравнительно низких энерго- и трудозатратах. Разработке эффективной технологии культивирования глубинной биомассы P. сitrinopileatus для внедрения в производство белковых продуктов должно предшествовать изучение характера роста продуцента, создание математической модели для прогнозирования роста и установления оптимальных условий культивирования, что и явилось целью настоящей работы.
Объектом исследования являлся штамм: РС-1.2 ксилотрофного базидиомицета Pleurotus citrinopileatus (P. сitrinopileatus) – вешенка лимонная, чистая культура которого была выделена из коммерческих плодовых тел. Систематическое положение объекта исследования: царство Fungi; отдел Basidiomycota; класс Agaricomycetes; подкласс Agaricomycetidae; порядок Agaricales; семейство Pleurotaceae; род Pleurotus; вид Pleurotus.
2. Методы и принципы исследования
Глубинное культивирование проводили в стационарном лабораторном биореакторе «CeCa-Cx650, Великобритания» при температуре 26 оС, pH 5,0 и непрерывном перемешивании путем барботирования стерильным воздухом (расход воздуха 100 л/ч на 1 л среды). Среду предварительно стерилизовали в автоклаве в течение 30 минут при 0,5 кгс/см2. В качестве питательной среды использовали гидролизат растительного сырья с массовой долей редуцирующих веществ не менее 3%.
Для определения прироста биомассы P. citrinopileatus каждые 12 часов отбирали пробу культуральной жидкости, объемом 10 мл. Затем пробу центрифугировали, биомассу (осадок) промывали дистиллированной водой, затем снова центрифугировали. Осадок высушивали и взвешивали.
Для построения математической модели эксперимента культивирования P. citrinopileatus рассчитывали: средние значения и стандартные ошибки опытов; дисперсию воспроизводимости; однородность дисперсий по критерию Кохрена; стандартную ошибку модели; коэффициент детерминации; адекватность модели по критерию Фишера и нормальное распределение ошибок по критерию Фроцини , .
Культивирование проводили при засевной концентрации мицелия – 1 г/л; начальной концентрации субстрата – 30 г/л. Время культивирования составило 120 ч; субстратная константа – 4; удельная скорость роста – 0,037 ч-1.
Одновременно прирост биомассы P. citrinopileatus рассчитывали с помощью уравнения Моно :
где:
X – предельное накопление биомассы, г/л;
X0 – засевная концентрация мицелия, г/л;
µm – удельная скорость роста, ч-1;
S0 – начальная концентрация субстрата, г/л;
Ks – субстратная константа;
t – время культивирования, ч.
В таблице приведены экспериментальные и расчетные данные по накоплению биомассы в ходе глубинного культивирования, которые послужили исходными для построения графиков, характеризующих рост биомассы (рисунок 1).
Таблица 1 - Расчетные и экспериментальные данные по накоплению биомассы P. citrinopileatus
t, ч | 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 | 120 |
Xрасч., г/л а.с.м. | 1,48 | 2,19 | 3,24 | 4,79 | 7,09 | 10,49 | 15,52 | 22,97 | 33,98 | 50,28 |
Xэкс., г/л а.с.м. | 1,15 | 1,95 | 2,85 | 4,95 | 7,70 | 10,35 | 15,10 | 15,20 | 15,20 | 15,15 |
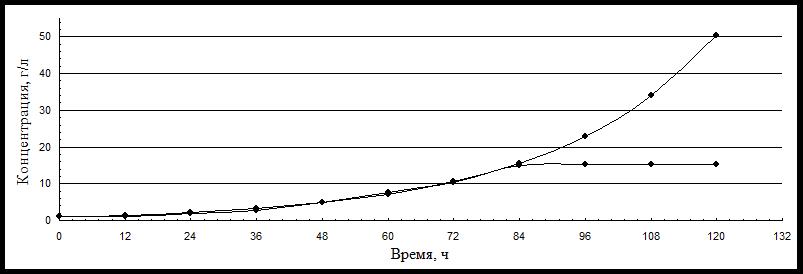
Рисунок 1 - Изменение расчетной и экспериментальной концентрации биомассы в ходе культивирования
Примечание: 1 – расчетная концентрация биомассы 1 г/л; 2 – экспериментальная концентрация биомассы 1 г/л
В зависимости от используемого режима культивирования и конструкции биореактора на этой стадии выращивания культуры производится либо полный слив культуральной жидкости с сепарацией биомассы, либо частичный слив культуральной жидкости с доливом свежей питательной среды до рабочего объема биореактора.
Данные рисунка 1 свидетельствуют, что экспериментальная и расчетная кривые практически совпадают. Это дает основание утверждать, что уравнение Моно удовлетворительно описывает характер процесса роста глубинной культуры P. citrinopileatus и позволяет применить это уравнение для построения математической модели процесса роста:
Для проверки адекватности и однородности математической модели была проведена обработка экспериментальных данных и рассчитаны: дисперсия воспроизводимости экспериментальных результатов измерения роста биомассы – 0,065 и стандартная ошибка воспроизводимости экспериментальных данных – 0,256.
3. Основные результаты
В ходе проверки гипотезы однородности дисперсий экспериментов, при 5% уровне значимости были найдены: расчётное значение критерия Кохрена – 0,244 и критическое значение критерия Кохрена – 0,602 (см. рис. 2).
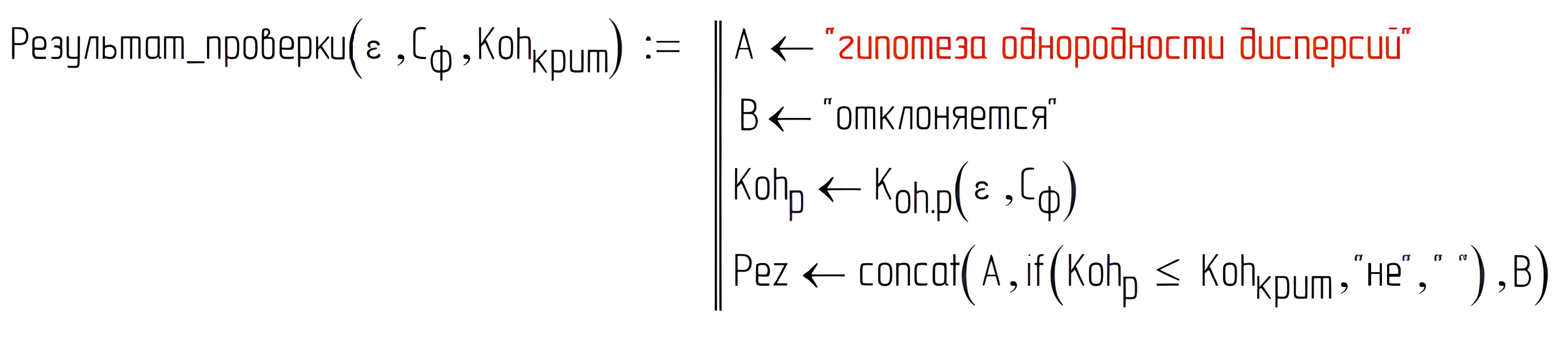
Рисунок 2 - Результат проверки гипотеза однородности дисперсий по критерию Кохрена
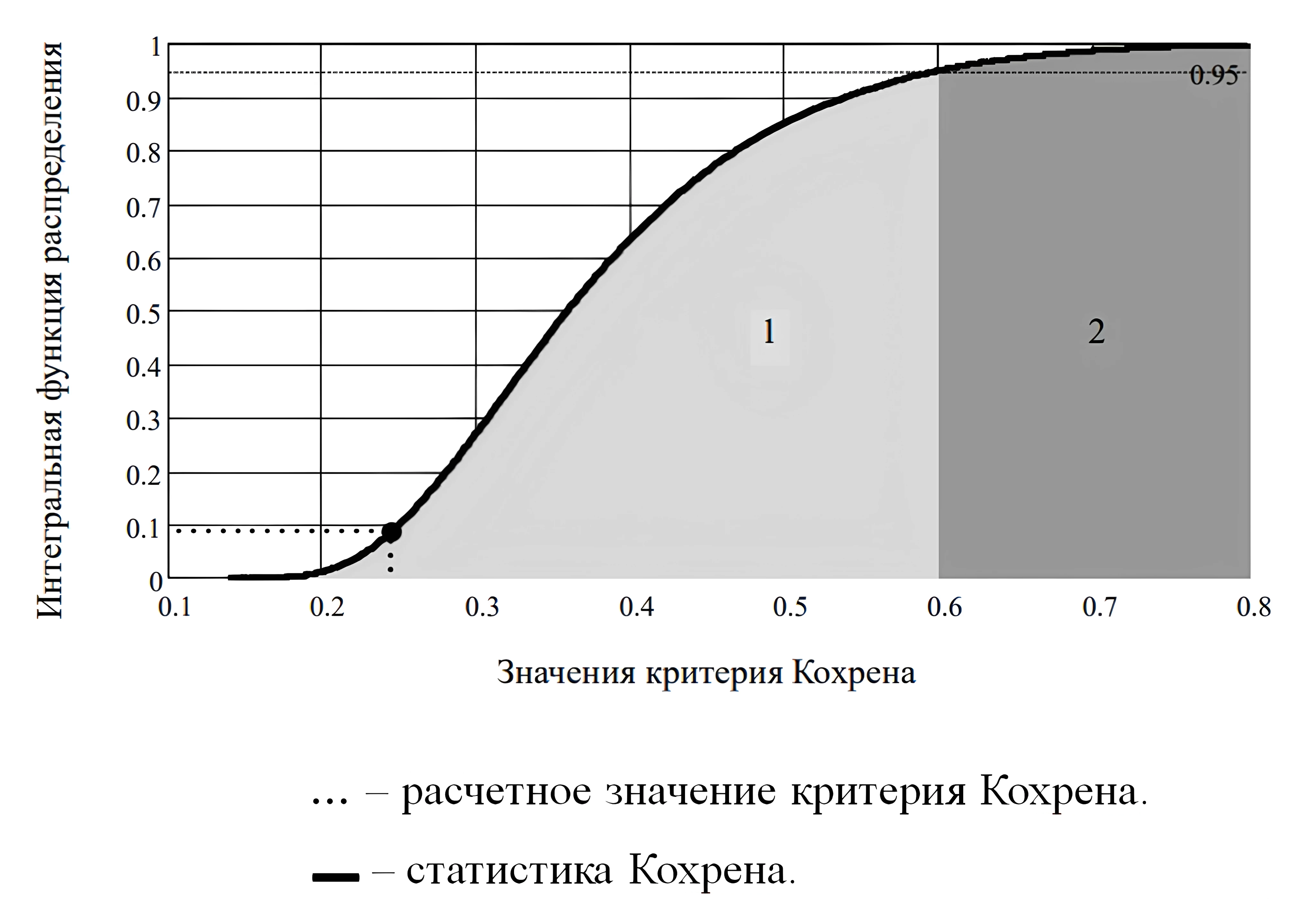
Рисунок 3 - Интегральная функция распределения статистики Кохрена
Примечание: 1 – область принятия гипотезы однородности; 2 – область отклонения гипотезы однородности
А : = “гипотеза адекватности модели”
В : = “отклоняется”
Результат проверки:=concat(A,if(Fp≤Fк”не”,” ”),B)
Результат проверки = «гипотеза адекватности модели не отклоняется».
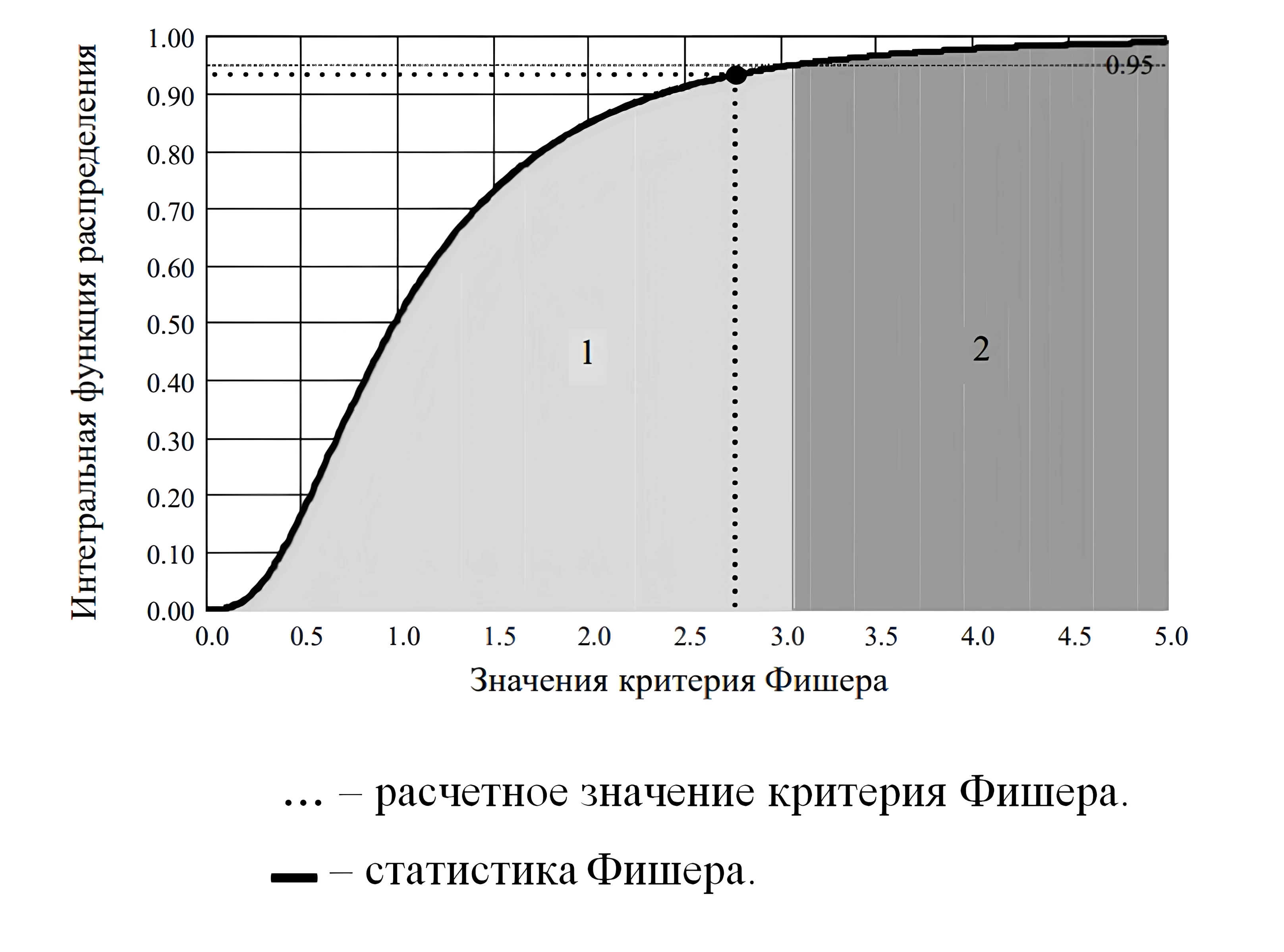
Рисунок 4 - Интегральная функция распределения статистики Фишера
Примечание: 1 – область принятия гипотезы адекватности; 2 – область отклонения гипотезы адекватности
Следующим этапом настоящей работы было нахождение интегральной функции распределения ошибок (рисунок 5).
Из графического представления интегральной функции распределения ошибок эксперимента видно, что ошибки проведенного эксперимента находятся в области допустимых значений, что еще раз подтверждает адекватность использования разработанной математической модели (1) для описания процесса роста глубинной культуры P. citrinopileatus.
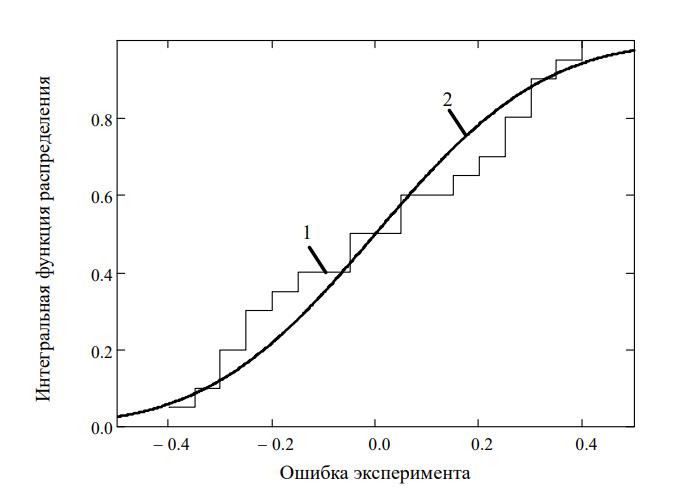
Рисунок 5 - Интегральная функция распределения ошибки эксперимента
Примечание: 1– эмпирическая; 2 – нормальная
Результат проверки нормальности распределения ошибок по критерию Фроцини:
Результат : = concat(“гипотеза нормальности”,if(Fp≤Fкр,”не”,” ”),”отклоняется”)
Результат =”гипотеза нормальности не отклоняется”
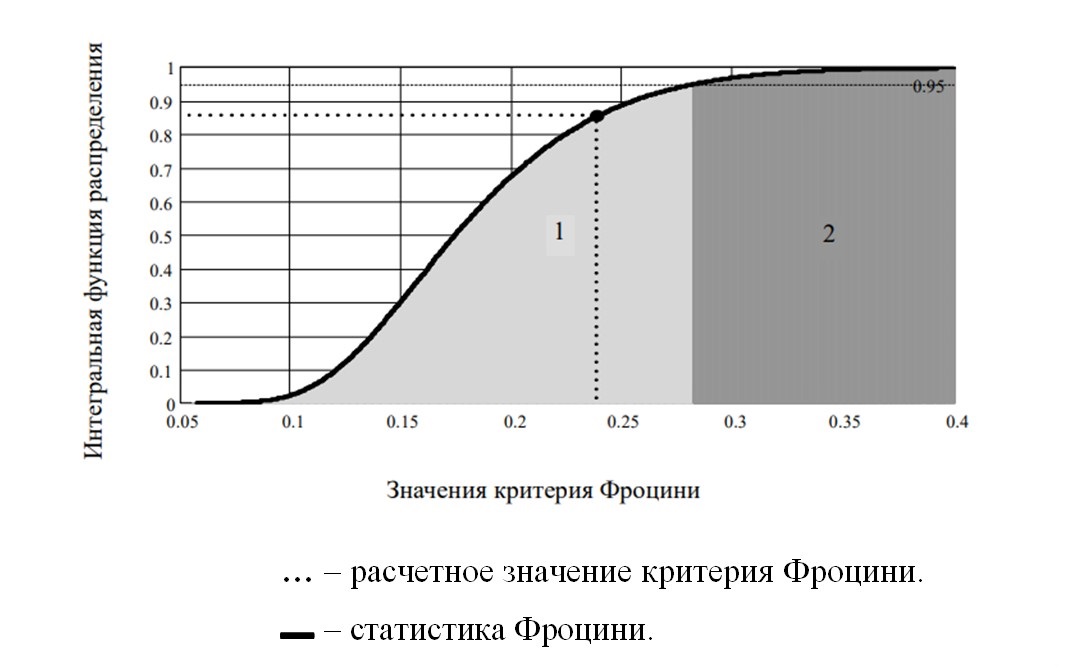
Рисунок 6 - Интегральная функция распределения ошибок эксперимента для прироста биомассы
Примечание: 1 – область принятия гипотезы нормальности; 2 – область отклонения гипотезы нормальности
Для построения кривых роста культуры с различной засевной концентрацией (рисунок 7) используем уравнение Моно в интегральной форме .
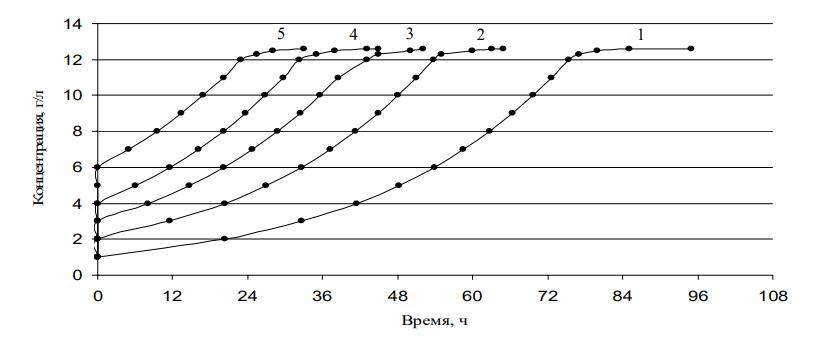
Рисунок 7 - Кривые роста с различной засевной концентрацией мицелия
Примечание: 1 – засевная концентрация 1 г/л; 2 – засевная концентрация 2 г/л; 3 – засевная концентрация 3 г/л; 4 – засевная концентрация 4 г/л; 5 – засевная концентрация 5 г/л
На основании экспериментальных данных построена кривая роста глубинной культуры Pleurotus citrinopileatus при засевной концентрации 1 г/л. Показано, что кривую роста точно описывает уравнение Моно. Разработана математическая модель роста глубинной культуры. Проверена ее однородность и адекватность.
4. Заключение
Применение разработанной математической модели позволяет характеризовать поведение культуры в глубинных условиях, устанавливать оптимальную начальную концентрацию мицелия в биореакторе, прогнозировать время и скорость накопления максимального количества биомассы.
