МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ГЛУБИННОГО КУЛЬТИВИРОВАНИЯ БИОМАССЫ PLEUROTUS CITRINOPILEATUS
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ГЛУБИННОГО КУЛЬТИВИРОВАНИЯ БИОМАССЫ PLEUROTUS CITRINOPILEATUS
Аннотация
Данная работа посвящена математическому описанию проведённого глубинного культивирования такого объекта исследования, как РС-1.2 ксилотрофного базидиомицета Pleurotus citrinopileatus (P. сitrinopileatus) – вешенка лимонная, чистая культура которого была выделена из коммерческих плодовых тел.
Сам эксперимент – глубинное культивирование, проводили в стационарном лабораторном биореакторе «CeCa-Cx650, Великобритания» при температуре 26 оС, pH 5,0 и непрерывном перемешивании путем барботирования стерильным воздухом.
На основании экспериментальных данных построена кривая роста глубинной культуры Pleurotus citrinopileatus при засевной концентрации 1 г/л. Показано, что кривую роста точно описывает уравнение Моно. Разработана математическая модель роста глубинной культуры. Проверена ее однородность и адекватность. Применение разработанной математической модели позволяет характеризовать поведение культуры в глубинных условиях, устанавливать оптимальную начальную концентрацию мицелия в биореакторе, прогнозировать время и скорость накопления максимального количества биомассы при различных засевных концентрациях.
1. Введение
В современном обществе белок является наиболее дефицитным компонентом пищи. Ценность пищевого белка определяется схожестью его аминокислотного состава с аминокислотным составом белков потребляющего его организма, что позволяет последнему активно усваивать и использовать подобные продукты в разнообразных метаболических процессах. В последние десятилетия значительное внимание исследователей в качестве продуцентов белка привлекают базидиальные грибы как источник белка, богатого незаменимыми аминокислотами.
Одним из перспективных продуцентов для получения грибного белка, является представитель рода Pleurotus – вешенка лимонная. Этот гриб, как в природных условиях, так и в культуре, непатогенен, обладает высокой пищевой ценностью и способен эффективно утилизировать разнообразные растительные субстраты.
Известно, что в плодовых телах вешенки лимонной (P. сitrinopileatus) наряду с белком, содержатся и биологически активные вещества, способные не только предупреждать, но и лечить широкий спектр заболеваний. Так, исследования последних лет , , свидетельствуют, что этот гриб обладает способностью снижать уровень глюкозы в крови человека, оказывает противоопухолевое действие, повышает иммунную устойчивость организма.
Сегодня показано, что культивируемый в глубинных условиях мицелий Pleurotus не уступает, а в ряде случаев по содержанию белка превосходит их плодовые тела , , . При этом глубинный мицелий имеет ряд преимуществ перед плодовым телом, из которых наиболее важные – чистота и стабильный химический состав. Таким образом, глубинное культивирование биомассы мицелия P. сitrinopileatus является одним из перспективных направлений получения пищевого и кормового белка , , .
Процесс получения мицелия по сравнению с выращиванием плодовых тел более высокопроизводителен при сравнительно низких энерго- и трудозатратах. Разработке эффективной технологии культивирования глубинной биомассы P. сitrinopileatus для внедрения в производство белковых продуктов должно предшествовать изучение характера роста продуцента, создание математической модели для прогнозирования роста и установления оптимальных условий культивирования, что и явилось целью настоящей работы.
Объектом исследования являлся штамм: РС-1.2 ксилотрофного базидиомицета Pleurotus citrinopileatus (P. сitrinopileatus) – вешенка лимонная, чистая культура которого была выделена из коммерческих плодовых тел. Систематическое положение объекта исследования: царство Fungi; отдел Basidiomycota; класс Agaricomycetes; подкласс Agaricomycetidae; порядок Agaricales; семейство Pleurotaceae; род Pleurotus; вид Pleurotus.
2. Методы и принципы исследования
Глубинное культивирование проводили в стационарном лабораторном биореакторе «CeCa-Cx650, Великобритания» при температуре 26 оС, pH 5,0 и непрерывном перемешивании путем барботирования стерильным воздухом (расход воздуха 100 л/ч на 1 л среды). Среду предварительно стерилизовали в автоклаве в течение 30 минут при 0,5 кгс/см2. В качестве питательной среды использовали гидролизат растительного сырья с массовой долей редуцирующих веществ не менее 3%.
Для определения прироста биомассы P. citrinopileatus каждые 12 часов отбирали пробу культуральной жидкости, объемом 10 мл. Затем пробу центрифугировали, биомассу (осадок) промывали дистиллированной водой, затем снова центрифугировали. Осадок высушивали и взвешивали.
Для построения математической модели эксперимента культивирования P. citrinopileatus рассчитывали: средние значения и стандартные ошибки опытов; дисперсию воспроизводимости; однородность дисперсий по критерию Кохрена; стандартную ошибку модели; коэффициент детерминации; адекватность модели по критерию Фишера и нормальное распределение ошибок по критерию Фроцини , .
Культивирование проводили при засевной концентрации мицелия – 1 г/л; начальной концентрации субстрата – 30 г/л. Время культивирования составило 120 ч; субстратная константа – 4; удельная скорость роста – 0,037 ч-1.
Одновременно прирост биомассы P. citrinopileatus рассчитывали с помощью уравнения Моно :
где:
X – предельное накопление биомассы, г/л;
X0 – засевная концентрация мицелия, г/л;
µm – удельная скорость роста, ч-1;
S0 – начальная концентрация субстрата, г/л;
Ks – субстратная константа;
t – время культивирования, ч.
В таблице приведены экспериментальные и расчетные данные по накоплению биомассы в ходе глубинного культивирования, которые послужили исходными для построения графиков, характеризующих рост биомассы (рисунок 1).
Таблица 1 - Расчетные и экспериментальные данные по накоплению биомассы P. citrinopileatus
t, ч | 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 | 120 |
Xрасч., г/л а.с.м. | 1,48 | 2,19 | 3,24 | 4,79 | 7,09 | 10,49 | 15,52 | 22,97 | 33,98 | 50,28 |
Xэкс., г/л а.с.м. | 1,15 | 1,95 | 2,85 | 4,95 | 7,70 | 10,35 | 15,10 | 15,20 | 15,20 | 15,15 |
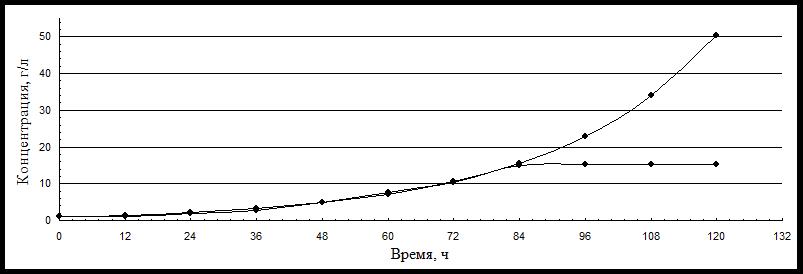
Рисунок 1 - Изменение расчетной и экспериментальной концентрации биомассы в ходе культивирования
Примечание: 1 – расчетная концентрация биомассы 1 г/л; 2 – экспериментальная концентрация биомассы 1 г/л
В зависимости от используемого режима культивирования и конструкции биореактора на этой стадии выращивания культуры производится либо полный слив культуральной жидкости с сепарацией биомассы, либо частичный слив культуральной жидкости с доливом свежей питательной среды до рабочего объема биореактора.
Данные рисунка 1 свидетельствуют, что экспериментальная и расчетная кривые практически совпадают. Это дает основание утверждать, что уравнение Моно удовлетворительно описывает характер процесса роста глубинной культуры P. citrinopileatus и позволяет применить это уравнение для построения математической модели процесса роста:
Для проверки адекватности и однородности математической модели была проведена обработка экспериментальных данных и рассчитаны: дисперсия воспроизводимости экспериментальных результатов измерения роста биомассы – 0,065 и стандартная ошибка воспроизводимости экспериментальных данных – 0,256.
3. Основные результаты
В ходе проверки гипотезы однородности дисперсий экспериментов, при 5% уровне значимости были найдены: расчётное значение критерия Кохрена – 0,244 и критическое значение критерия Кохрена – 0,602 (см. рис. 2).
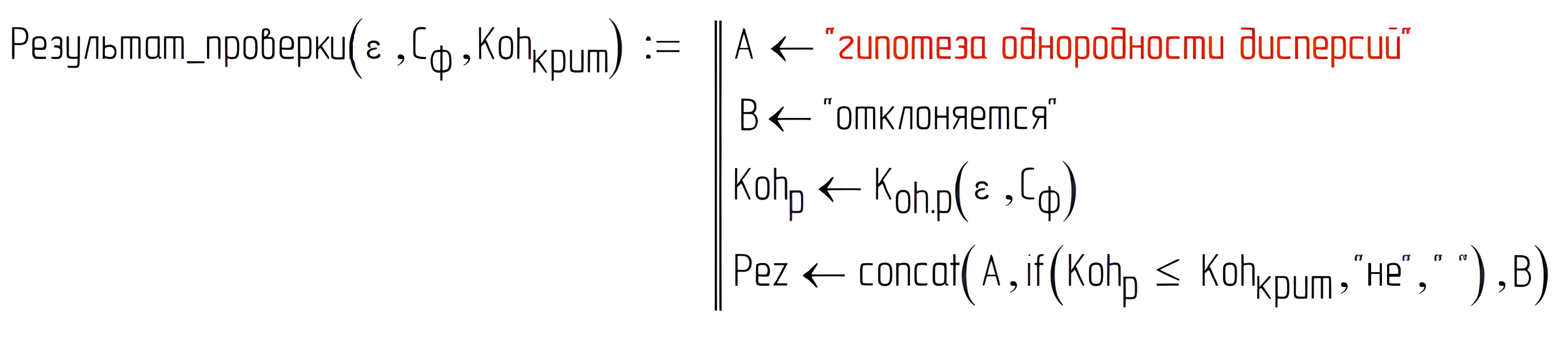
Рисунок 2 - Результат проверки гипотеза однородности дисперсий по критерию Кохрена
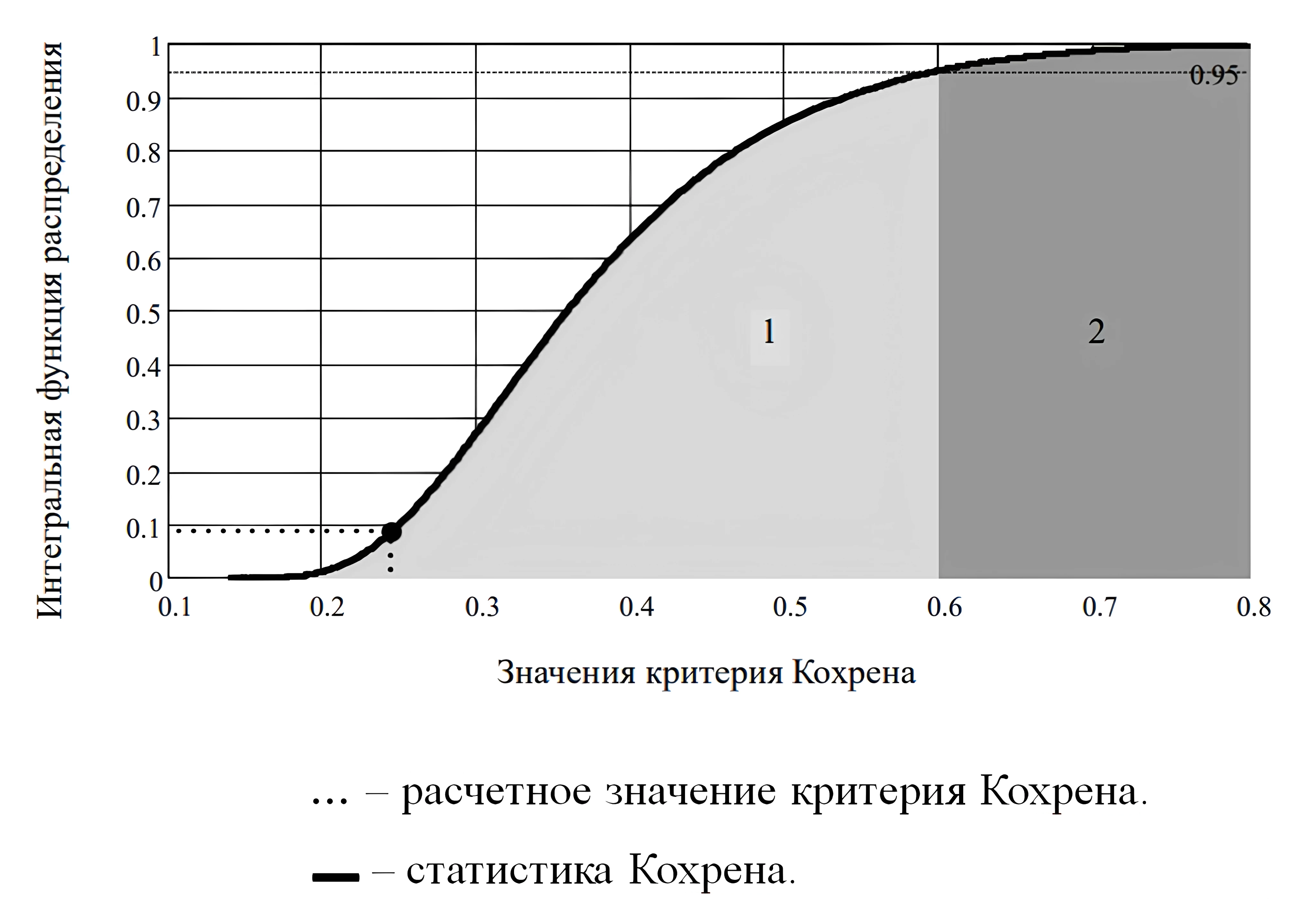
Рисунок 3 - Интегральная функция распределения статистики Кохрена
Примечание: 1 – область принятия гипотезы однородности; 2 – область отклонения гипотезы однородности
А : = “гипотеза адекватности модели”
В : = “отклоняется”
Результат проверки:=concat(A,if(Fp≤Fк”не”,” ”),B)
Результат проверки = «гипотеза адекватности модели не отклоняется».
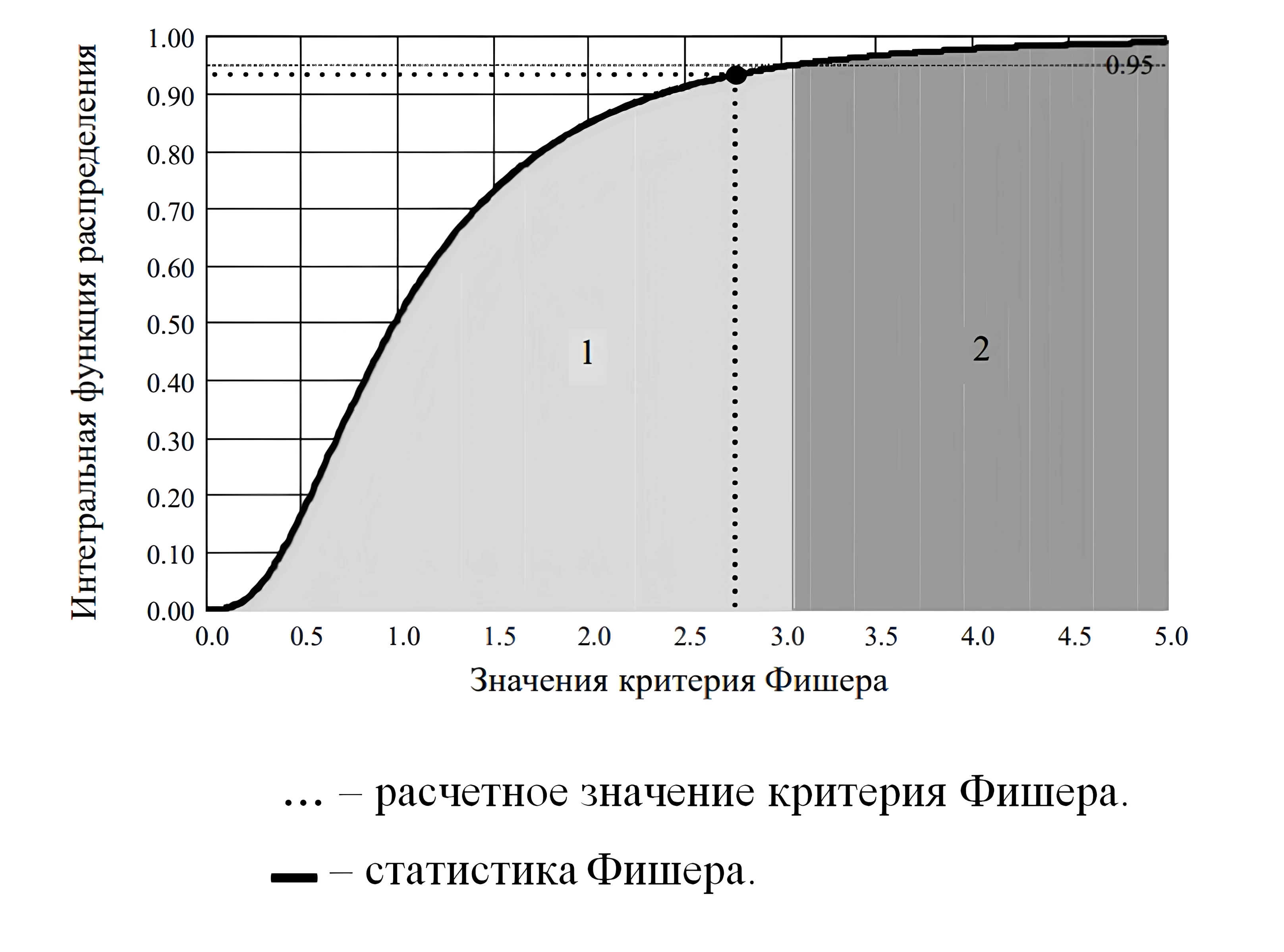
Рисунок 4 - Интегральная функция распределения статистики Фишера
Примечание: 1 – область принятия гипотезы адекватности; 2 – область отклонения гипотезы адекватности
Следующим этапом настоящей работы было нахождение интегральной функции распределения ошибок (рисунок 5).
Из графического представления интегральной функции распределения ошибок эксперимента видно, что ошибки проведенного эксперимента находятся в области допустимых значений, что еще раз подтверждает адекватность использования разработанной математической модели (1) для описания процесса роста глубинной культуры P. citrinopileatus.
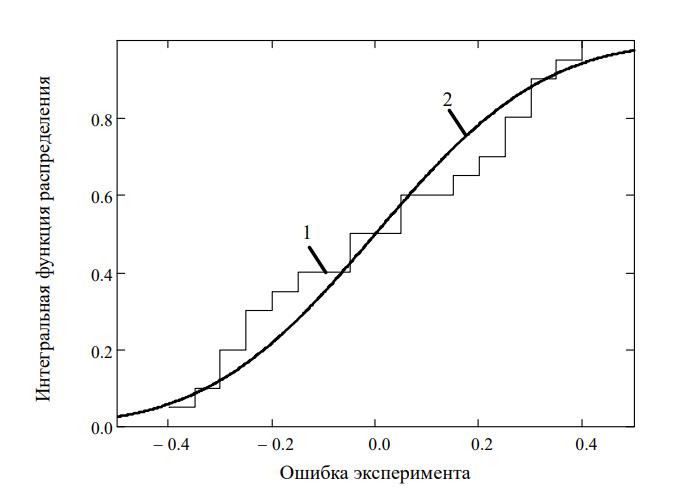
Рисунок 5 - Интегральная функция распределения ошибки эксперимента
Примечание: 1– эмпирическая; 2 – нормальная
Результат проверки нормальности распределения ошибок по критерию Фроцини:
Результат : = concat(“гипотеза нормальности”,if(Fp≤Fкр,”не”,” ”),”отклоняется”)
Результат =”гипотеза нормальности не отклоняется”
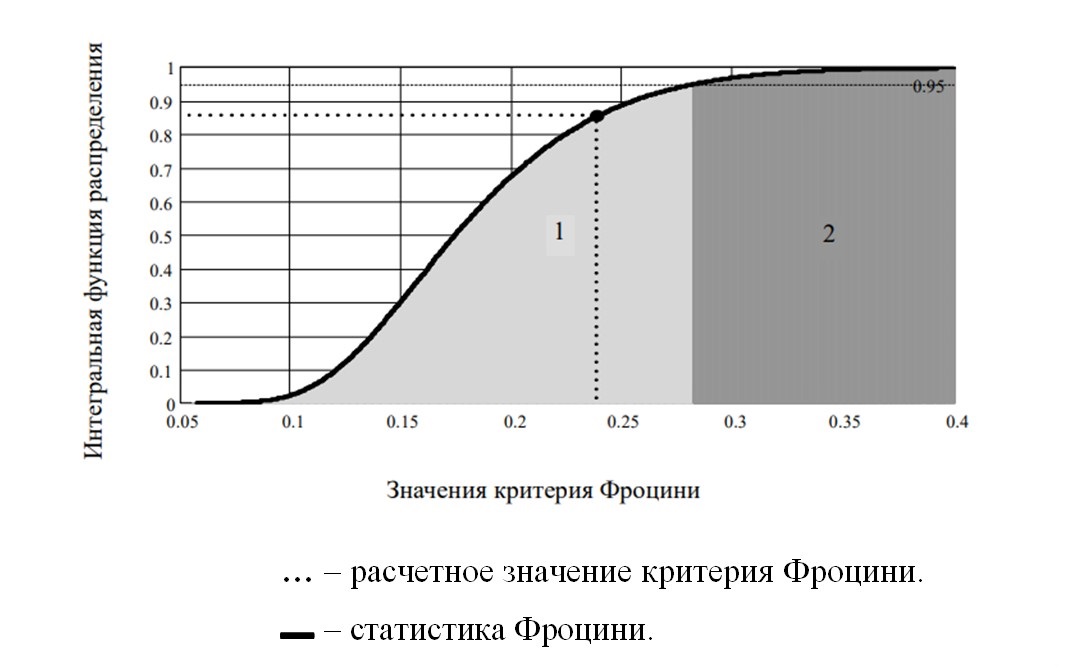
Рисунок 6 - Интегральная функция распределения ошибок эксперимента для прироста биомассы
Примечание: 1 – область принятия гипотезы нормальности; 2 – область отклонения гипотезы нормальности
Для построения кривых роста культуры с различной засевной концентрацией (рисунок 7) используем уравнение Моно в интегральной форме .
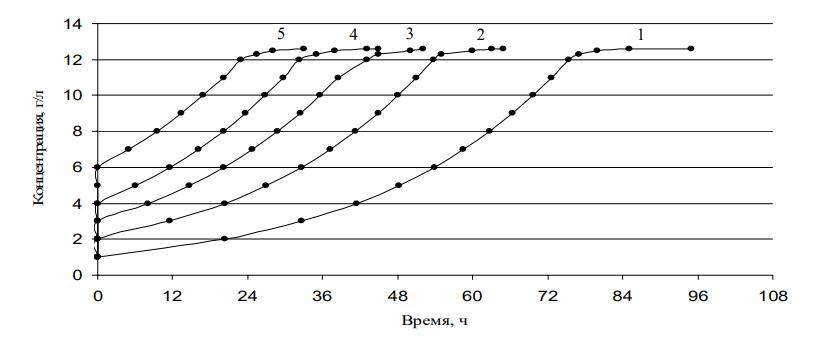
Рисунок 7 - Кривые роста с различной засевной концентрацией мицелия
Примечание: 1 – засевная концентрация 1 г/л; 2 – засевная концентрация 2 г/л; 3 – засевная концентрация 3 г/л; 4 – засевная концентрация 4 г/л; 5 – засевная концентрация 5 г/л
На основании экспериментальных данных построена кривая роста глубинной культуры Pleurotus citrinopileatus при засевной концентрации 1 г/л. Показано, что кривую роста точно описывает уравнение Моно. Разработана математическая модель роста глубинной культуры. Проверена ее однородность и адекватность.
4. Заключение
Применение разработанной математической модели позволяет характеризовать поведение культуры в глубинных условиях, устанавливать оптимальную начальную концентрацию мицелия в биореакторе, прогнозировать время и скорость накопления максимального количества биомассы.
